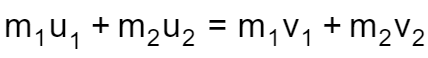Conservation of Momentum Calculator
Momentum is one of the few fundamental quantities that, in isolated systems, can't change over time: learn the consequences and applications of this property with our conservation of momentum calculator.
In this article, you will learn:
- What is momentum;
- What is the conservation of momentum law;
- The equations of the conservation of momentum in different types of collisions;
- How to use our conservation of momentum calculator.
What is momentum?
Momentum is the product of mass and velocity and corresponds to the quantity of motion of a massive body. The heavier or (and) faster an object is, the higher its momentum, leading to various consequences. For example:
- A body with high momentum is harder to slow down or stop;
- The momentum of a body is directly responsible for the effect of an impact; or
- A rocket moves thanks to the momentum of its exhaust.
Momentum is a vector quantity: we can associate a direction and a magnitude due to the presence of the body's velocity. This is a crucial feature for the understanding of the conservation of momentum.
If you want to learn more about momentum, check our other tool that explains how to calculate linear momentum.
What is the conservation of momentum?
In an isolated system (without external forces acting on it), the total momentum inside the system can't change. Another way to state this law is to say that the sum of the momentum of each body in a closed system doesn't change.
This law dictates the result of impacts between bodies.
The conservation of momentum in different types of impact
An impact between two (or more) bodies sees the transfer of various quantities: momentum, kinetic energy, and so on. According to how these quantities transfer, we can identify three types of collisions:
- Perfectly elastic collisions;
- Partly elastic collisions; and
- Perfectly inelastic collisions.
Let's analyze them in detail.
Perfectly elastic collisions
In such a collision, both the momentum and the kinetic energy are conserved. Hard, rigid objects nicely approximate elastic collision. Think of pool balls that are full spheres (we have a calculator dedicated to sphere volume formula). If you consider only two bodies, with initial masses and , and velocities and , and make them collide, their velocity changes. Thanks to the momentum conservation law, we can write down the fundamental equation controlling the collision:
We can compute the final velocities by adding to this equation the conservation of the kinetic energy. We would obtain the following equations:
Partly elastic collisions
In this collision, only the momentum is conserved, while the kinetic energy can dissipate. This collision described here is non-ideal: some of the energy in the collision convert into heat or deformation of the bodies. We can't define equations for the calculations of the final speed; however, the equation for the conservation of momentum still holds:
Perfectly inelastic collisions
In this type of collision, the two bodies somehow stick together, moving, after the impact, with the same velocity (both in magnitude and direction). Some of the kinetic energy is lost; however, the momentum is still entirely conserved.
We can write a slightly modified equation for the conservation of momentum:
Where is the final velocity.
The consequences of the law of conservation of momentum
The law of conservation of momentum allows you to calculate and understand many problems in physics. Think of rockets: even though there's not really an impact, we can apply the law. Take the rocket in an initial state where it lies with zero speed and a full fuel tank: the system's total momentum is zero. The fuel ignites and exits from the back: doing this, it acquires momentum. The rocket moves in the opposite direction to conserve the zero momentum of the system. The gases from the exhaust move at a far higher speed than the rocket itself but have a decisively lower mass — which balances the rocket's lower speed and higher mass.
A Newton's cradle is a good (but not perfect) example of the conservation of momentum. That desk toy uses almost elastic impacts to transfer momentum from one end to the other of a series of identical spheres.
How to use our conservation of momentum calculator
Our conservation of momentum calculator allows you to calculate the outcome of one of the three types of collisions. Choose the type in the variable collision type (if you don't know it, select "don't know"), and insert the known quantities. We will tell you all we can about the outcome of the collision.
If you, by chance, consider a problem of a ball rolling down the slope, you might find the slope calculator very useful. Be sure to check it!