Snell's Law Calculator

This Snell's law calculator will help you trace the refracted light ray when it enters a medium with a different refractive index. You can also determine the critical angle of the medium, provided the second medium has a smaller refractive index than the first.

In this article, we shall learn how to find the angle of refraction using Snell's law of refraction. We shall also discuss what critical angle and its formula are.

If you need to calculate refractive indices, use our index of refraction calculator.

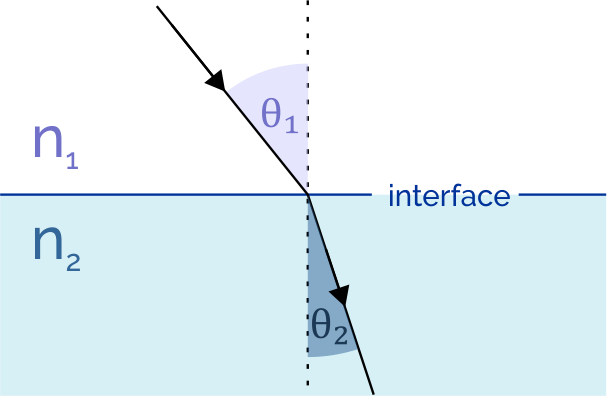
Refraction is the phenomenon by which a wave changes direction when moving from one medium to another. Although we commonly observe this in light, other waves like sound also experience this.

When light enters a medium of lower refractive index, it moves faster and refracts away from the boundary normal. When it enters a medium of higher refractive index, its speed reduces, and it refracts towards the boundary normal. We notice this redirection (or displacement in its trajectory) by a change in the angle of refraction.

Snell's law establishes a relationship between the refractive indices and the angles of incidence and refraction:

where:

• $n_1$ is the refractive index of the first medium;

• $\theta_1$ is the angle of incidence;

• $n_2$ is the refractive index of the second medium; and

• $\theta_2$ is the angle of refraction.

Using this Snell's law formula, we can calculate the angle of refraction if we know the refractive indices and the incident angle.

For example, let's determine the path of a light ray incident at an angle of $30\degree$ on a glass pane with a refractive index of $1.5$. If we assume the air's refractive index to be $1$, we can calculate the angle of refraction as:

We can therefore treat the following version of Snell's law of refraction as the angle of refraction formula:

Find out what happens when light travels through three mediums of different refractive indices with our thin film optical coating calculator.

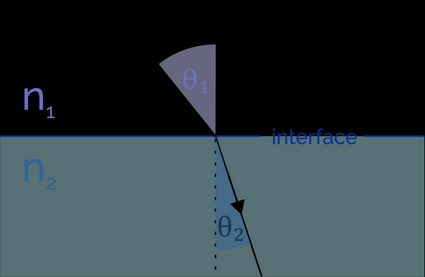
When light passes from a higher refractive index medium to a lower refractive index one, we can observe refraction up to a certain angle of incidence. After this angle, all light incident on the interface is reflected back into the medium with a higher refractive index. This exciting phenomenon is total internal reflection, which makes high-speed optical fiber networks possible.

We define the critical angle as the minimum incident angle required for total internal reflection. Alternatively, we can also define it as the maximum incident angle for which we can observe refraction. At this angle, the refracted ray travels parallel to the interface $(\theta_2 = 90\degree)$.

With this understanding, let's derive a formula for the critical angle $\theta_c$ from Snell's law formula:

If you're confusing critical angle with Brewster angle, our Brewster angle calculator is here to help.

We pride ourselves on the versatility of Snell's law calculator. Here are some instructions to put it to good use:

1. Select the two mediums from their respective lists. This action will autofill values for their refractive indices. But don't let that stop you from entering custom values if required.

2. • Enter the angle of incidence to determine the angle of refraction using the refraction angle formula.
   • Provide the angle of refraction to determine the incident angle.