Electric Potential Calculator

Our electric potential calculator can obtain the electric potential at any distance from a single point charge or a number of point charges (up to ten).

If you don't know what the electric potential is, don't worry. Within this short article, we will cover:

• Electric potential definition;
• Electric potential formula/equation;
• Electric potential due to a point charge; and
• Electric potential due to a system of point charges.

Let's start!

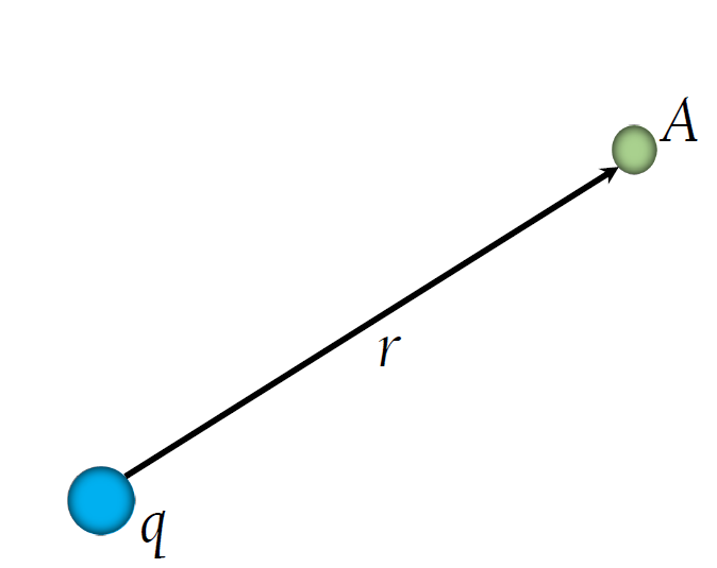
We define the electric potential of a point charge at a point in space as the work required to bring a $1\ \text{C}$ charge from infinity to that location.

Sounds confusing? Let's do some math first so you can start working with the electric potential calculator.

Assume we had two positive point charges, $q$ and $Q$, separated by a distance of $r$.

If you remember, Coulomb's law describes the force $F$ between these particles:

where $k_{e}$ is Coulomb's constant.

Now, assume we tried to bring the charges closer by moving $q$ from $r_{1}$ to $r_{2}$ ($r_{1} > r_{2}$). For that, we would need to do work against this repulsive force:

by integrating between $r_{1}$ and $r_{2}$ we get:

Lastly, if we replace one of the charges with a unit test charge (a $1\ \text{C}$ positive charge) and set our initial point at infinity, we obtain the electric potential equation for a point charge:

This potential depends only on $r$ and $Q$, and its unit is the volt (V).

We can extend this definition to a system of multiple point charges easily.

The electric potential of multiple point charges $q_{i}$ at a point in space is simply the vector sum of each individual electric potential:

With our electric potential calculator, you can input up to ten point charges and it will output the resulting electric potential at any point. Give it a try!