Projectile Motion Calculator
Welcome to the projectile motion calculator, a kinematic tool that will help you to solve projectile equations in physics and calculate distance, maximum height, time of flight, and many more projectile parameters!
To learn more about the theory behind and solve the problems on your own, in the next section, we present the kinematic equations, which are the basis for the projectile equations such as the vertical velocity formula.
Click on the advanced mode to discover other additional parameters that could be useful.
🔎 With this tool, you can calculate the projectile motion parameters, but if you want to study the vertical position as a function of the horizontal displacement, use the trajectory calculator.
Kinematic equations
To understand the projectile equations, first, we must learn the equations used in kinematics calculations. Assuming constant acceleration:
- r = r0 + Vavgt
- Vavg = (V0 + V)/2 (for a = 0)
- V= V0 + rt
- r = r0 + V0t + at2/2
- V2 = V02 + 2a(r - r0)
where:
- r — position at the time t;
- r0 — initial position;
- V — velocity at the time t;
- vavg — average velocity;
- t — time; and
- a — acceleration
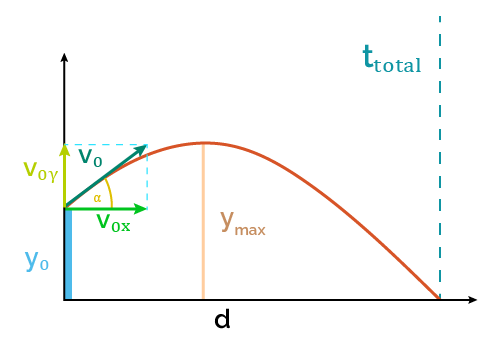
Flight parameters at a given time
To apply the previous equations to the projectile motion calculation, we have to consider some aspects of this type of motion:
- The horizontal component of acceleration is zero (ax = 0)
- The vertical component equals the negative of the gravity acceleration (ay = -g = -9.807 m/s2), assuming positive is up.
- Assuming the air resistance is negligible, the horizontal component of velocity remains constant (Vx = V0x)
- We can decompose the initial velocity into its horizontal and vertical components. As those components form right triangles, then:
- Horizontal velocity formula: V0x = V0 × cos(α)
- Vertical velocity formula: V0y = V0 × sin(α)
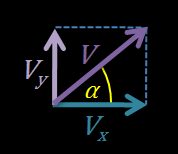
If the vertical velocity component is zero (α = 0°), then that's a case of horizontal projectile motion. If, on the other side, α = 90°, that's a case of free fall at zero initial velocity.
Considering the previous points, we can establish the flight parameters at a given time t:
Horizontal motion | x = x0 + Vxt |
Vx = V0x | |
Vertical motion | y = y0 + (1/2)(V0y + Vy)t |
Vy = V0y - gt | |
y = y0 + V0yt - gt2/2 | |
Vy2 = V0y2 - 2g(y - y0) |
Equations for projectile motion calculation
-
Angle of launch: If we know the initial velocity and one of its components, we can also calculate the angle of launch:
- α = arccos(V0x/V0) = arcsin(V0y/V0)
-
Maximum height: At this point, the projectile stops moving up and starts falling, so its vertical velocity component changes from positive to negative; therefore, Vy=0. For the time when Vy=0, we have:
- ymax = y0 + V0y²/(2g)
-
Horizontal distance traveled: if the problem you're solving in physics is calculating the distance traveled by the projectile, use the formula:
- d = Vxttotal = V0xttotal
-
Time of flight: Flight ends when the projectile hits the ground, which happens when y = 0:
- ttotal = [V0y + √(V0y² + 2gy0)]/g